Интегрированные сети ISDN
Приведенные коэффициенты, по сути, представляют
Таблица 4.5.14.2
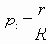
| Коэффициент | Название |
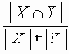 |
Коэффициент Дайса (dice) |
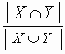 |
Коэффициент Джаккарда (jaccard) |
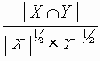 |
Косинусный коэффициент |
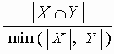 |
Коэффициент перекрытия |
Приведенные коэффициенты, по сути, представляют собой нормализованные варианты простого коэффициента соответствия.
Скажем несколько слов о функциях, определяющих степень различия между документами. Причины использования в системах поиска информации функций, определяющих степень различия между документами, вместо степени соответствия являются чисто техническими. Добавим, что любая функция оценки степени различия между документами d может быть преобразована в функцию, определяющую степень соответствия s следующим образом:
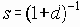
Если P – множество объектов, предназначенных для кластеризации, то функция D определения степени различия документов – это функция, ставящая в соответствие
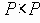
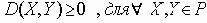
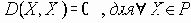
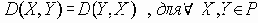
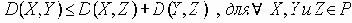
Четвертое свойство неявно отображает тот факт, что функция определения степени различия между документами является, в некоторой степени, функцией, определяющей “расстояние” между двумя объектами и, следовательно, логично предположить, что должна удовлетворять неравенству треугольника. Данное свойство выполняется практически для всех функций определения степени различия.
Пример функции, удовлетворяющей свойствам 1 – 4:
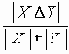
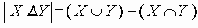
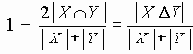
Наконец, представим функцию определения степени различия в альтернативной форме:
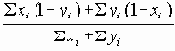
Используя векторное представление документов, для

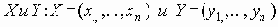
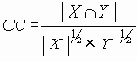
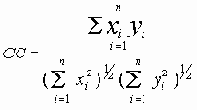
Скажем несколько слов о вероятностном подходе для функций, определяющих степень соответствия. Степень соответствия между объектами определяется по тому, насколько их распределения вероятности отличаются от статистически независимого.
Для определения степени соответствия используется ожидаемая взаимная мера информации. Для двух дискретных распределений вероятности
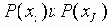
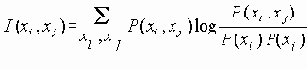
Если xi и xj - независимы, тогда
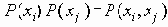
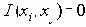
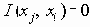

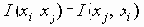
Функция
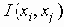
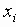
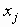

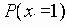
Та степень взаимосвязи, которая существует между индексными терминами i и j вычисляется затем функцией
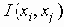
Были предложены и другие функции, похожие на описанную выше функцию
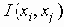
Как и в случае автоматической классификации документов, использование вероятностных методов при формировании кластеров содержит в себе достаточно высокий потенциал и представляет крайне интересную область для исследований.
Итак, для формирования кластеров необходимо использовать некую функцию соответствия для определения степени связи между парами документов из коллекции.
Постулируем теперь основную идею, на которой, собственно говоря, и построена вся теория кластерного представления коллекции документов. Гипотеза, приведшая к появлению кластерных методов, называется Гипотезой Кластеров и может быть сформулирована следующим образом: “Связанные между собой документы имеют тенденцию быть релевантными одним и тем же запросам”.
Базисом, на котором построены все системы автоматического поиска информации, является то, что документы, релевантные запросу, отличаются от нерелевантных документов.
Гипотеза кластеров указывает на целесообразность разделения документов на группы до обработки поисковых запросов. Естественно, она ничего не говорит о том, каким образом должно проводиться это разделение.
Проводился ряд исследований по поводу применения кластерных методов в поисковых системах. Некоторые отчеты приведены в работах Б. Литофски, Д. Крауча, Н. Привеса и Д. Смита, а также М. Фритше.
Кластерные методы, выбираемые для использования в экспериментальных поисковых системах должны удовлетворять некоторым определенным требованиям. Это:
Основной вывод из вышесказанного состоит в том, что любой кластерный метод, не удовлетворяющий приведенным условиям, не может производить сколько-нибудь значащие экспериментальные результаты. Надо сказать что, к сожалению, далеко не все работающие кластерные методы удовлетворяют приведенным требованиям. В основном, это происходит из-за значительных различий между реализованными методами кластеризации от теоретически разработанных ад-хок алгоритмов.
Другим критерием выбора является эффективность процесса создания кластеров с точки зрения производительности и требований к объему необходимого дискового пространства.
Необходимость учета данного критерия находится, естественно, в сильной зависимости от конкретных условий и требований.
Возможно, использование процедур фильтрации базы данных таким образом, что из базы данных будет удаляться информация об индексных терминах, встречающихся в более чем, скажем 80% проиндексированных документов. Таким образом, список стоп-слов будет динамически изменяющимся. Как уже говорилось, использование списка стоп-слов может приводить к 30% уменьшению размеров индексных файлов.
Для построения кластеров обычно используется два основных подхода:
В первом случае кластеры можно представить с помощью графов, построенных с учетом значений функции соответствия для каждой пары документов.
Рассмотрим некоторое множество объектов, которые должны быть кластеризованы. Для каждой пары объектов из данного множества вычисляется значение функции соответствия, показывающее насколько эти объекты сходны.
Если полученное значение оказывается больше величины заранее определенного порогового значения, то объекты считаются связанными. Вычислив значения функции соответствия для каждой пары объектов, строится граф, по сути, представляющий собой кластер. То есть определение кластера строится в терминах графического представления.
Список литературы
| 1 | Salton, G., “Automatic Text Analysis”, Science, 168, 335-343 (1970) |
| 2 | Luhn, H. P. “The automatic creation of literature abstracts”, IBM Journal of Research and Development, 2, 159-165 (1958) |
| 3 | Gerard Salton, Chris Buckley and Edward A. Fox, “Automatic Query Formulations in Information Retrieval”, Cornell University, http://cs-tr.cs.cornell.edu/ |
| 4 | Tandem Computers Inc. “Three Query Parsers”, http://oss2.tandem.com /search97/doc/srchscr/tpappc1.htm |
| 5 | Object Design Inc., “Persistent Storage Engine PSE-Pro documentation”, http://www.odi.com/ |
| 6 | Roger Whitney, “CS 660: Combinatorial Algorithms. Splay Tree”, San Diego State University. http://saturn.sdsu.edu:8080/~whitney/ |
